Quantum Metrology
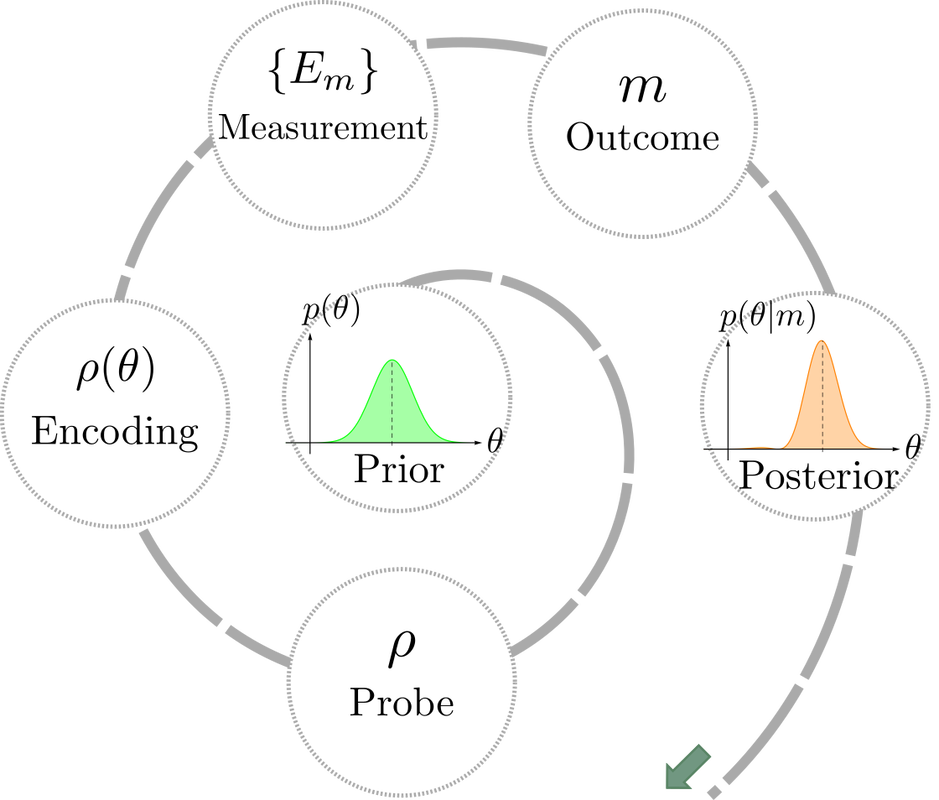
Quantum metrology exploits distinctive quantum features, such as entanglement, to enhance the estimation precision of parameters governing the dynamical evolution of the probe systems beyond that achievable by classical means. This enhancement is manifested in the form of a scaling gap in precision with respect to the available resources (the number of probe systems or the average input energy) between the corresponding optimal quantum and classical strategies, and depends on the specific encoding of the parameter in the Hamiltonian describing the evolution.
|
Metrology-Assisted Entanglement Distribution
In this project we have considered the distribution of high-dimensional entangled states to multiple parties via noisy channels and the subsequent probabilistic conversion of these states to desired target states using stochastic local operations and classical communication. In [Simon Morelli, David Sauerwein, Michalis Skotiniotis, and Nicolai Friis, Metrology-assisted entanglement distribution in noisy quantum networks, Quantum 6, 722 (2022)] we show that such state-conversion protocols can be enhanced by embedded channel-estimation routines at no additional cost in terms of the number of copies of the distributed states. The defining characteristic of our strategy is the use of those copies for which the conversion was unsuccessful for the estimation of the noise, thus allowing one to counteract its detrimental effect on the successfully converted copies. Although this idea generalizes to various more complex situations, we focus on the realistic scenario, where only finitely many copies are distributed and where the parties are not required to process multiple copies simultaneously. In particular, we investigate the performance of so-called one-successful-branch protocols, applied sequentially to single copies and an adaptive Bayesian estimation strategy. Finally, we compare our strategy to more general but less easily practically implementable strategies involving distillation and the use of quantum memories to process multiple copies simultaneously. |
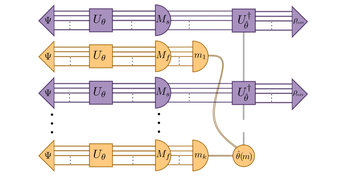
Illustration of a metrology-assisted entanglement-distribution protocol: in a probabilistic protocol, some "branches" are successful (violet), while the unsuccessful branches can be used to estimate potential noise channels, thus allowing one to apply suitable corrections to the successful branches.
|
|
Bayesian Estimation Using Gaussian States and Measurements
Bayesian analysis is a framework for parameter estimation that applies even in uncertainty regimes where the commonly used local (frequentist) analysis based on the Cramér–Rao bound (CRB) is not well defined. In particular, it applies when no initial information about the parameter value is available, e.g., when few measurements are performed. In [Simon Morelli, Ayaka Usui, Elizabeth Agudelo, and Nicolai Friis, Bayesian parameter estimation using Gaussian states and measurements, Quantum Sci. Technol. 6, 025018 (2021)] we consider three paradigmatic estimation schemes in continuous-variable (CV) quantum metrology (estimation odisplacements, phases, and squeezing strengths) and analyse them from the Bayesian perspective. For each of these scenarios, we have investigated the precision achievable with single-mode Gaussian states under homodyne and heterodyne detection. This allows us to identify Bayesian estimation strategies that combine good performance with the potential for straightforward experimental realization in terms of Gaussian states and measurements. Our results provide practical solutions for reaching uncertainties where local estimation techniques apply, thus bridging the gap to regimes where asymptotically optimal strategies can be employed. |
|
Flexible Metrology Using Cluster States
A particular question that I have been pursuing is, whether architectures for measurement-based quantum computation can be employed as flexible metrology devices. In this context, we have investigated the possibility of creating a versatile all-purpose device for quantum metrology based on 2D cluster states [Friis, Orsucci, Skotiniotis, Sekatski, Dunjko, Briegel, Dür, New J. Phys. 19, 063044 (2017)]. We demonstrated that the quadratic scaling advantage that can be obtained in quantum parameter estimation with respect to classical strategies is maintained and can be physically realized in this new paradigm integrating quantum metrology into setups for measurement-based quantum computation. In particular, our approach allows to achieve this scaling advantage for a number of estimation scenarios that require very different probe states and measurements. A presentation of this work can be found here (pdf). |
|
Gaussian Quantum Metrology
Another research interest within quantum metrology concerns estimation scenarios where the parameter of interest is encoded in Gaussian transformations, see [Friis, Skotiniotis, Fuentes, Dür, Phys. Rev. A 92, 022106 (2015)], and more generally in the connection between quantum metrology, quantum computing and quantum thermodynamics. A pdf presentation of this work can be found here. |
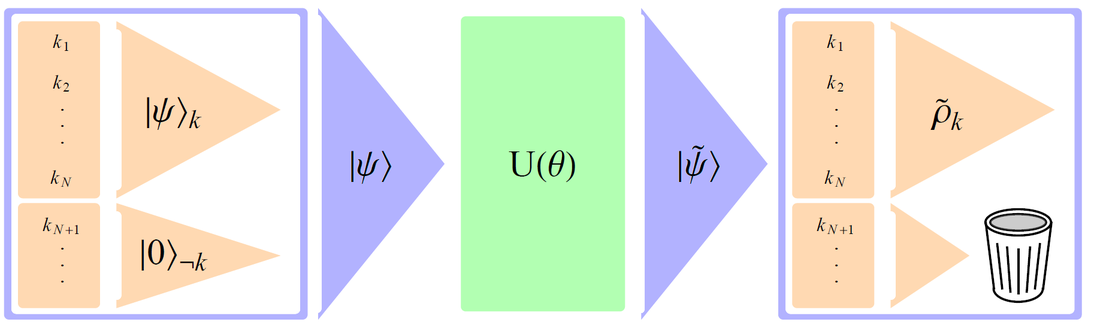
Parameter estimation scheme: A probe state |Ψ> is prepared, where we assume only subset k of modes can be controlled, while all other modes are prepared in the vacuum. The transformation U(ϴ) imprints the parameter ϴ on the state. A final measurement on the reduced state of the controlled modes provides information about ϴ.
|