Current Topics of Interest
|
Entanglement Detection and Certification
Entanglement is a concept that is both at the heart of foundational questions in quantum mechanics and at the core of many quantum technologies, from quantum communication to quantum computing. Entanglement manifests as correlations between measurement outcomes of two (or more) observers. For instance, measurements of the spin of two spin-1/2 particles along some pair of fixed directions, polarization measurements of two photons, or finding the valence electrons of trapped ions in particular energy levels. The feature that distinguishes entanglement from classical correlations is that these correlations persist for two (or more) complementary measurement bases, which forms the basis for phenomena such as the violation of Bell inequalities, However, checking (both mathematically, given some density operator describing a quantum system, and practically), can be challenging, and the quantification of entanglement via suitable figures of merit is generally even more complicated. In my research, I aim to develop techniques both for the theoretical characterization as well as for the experimental certification of entanglement, with the hopes of employing these tools for the characterization of quantum devices. More information on my work in this direction can be found here. |
|
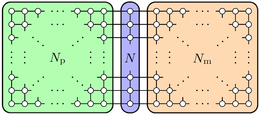
In this pillar of my current research, I am working on developing suitable benchmarking techniques, error-correction techniques assisted by reinforcement learning, and proof-of-concept demonstrations for nextgeneration ion-trap quantum computers that are interfaced with and supplemented by classical high-performance computing centres. Part of this research is a joint effort within the Flagship Project “High-Performance integrated Quantum Computing (HPQC)" by the Austrian Research Promotion Agency (FFG) that is being carried out by a consortium led by Thomas Monz and Martin Ringbauer at the University of Innsbruck. More details on this line of research are available here.
|
|
Quantum Thermodynamics (QT) is concerned with the investigation of phenomena such as thermalization and equilibration, heat engines, and foundations of thermodynamics in the quantum regime.The study of thermodynamics in the quantum domain provides an amazing example for the cross-fertilization between different areas of physics, involving classical thermodynamics and solid state physics, as well as quantum information and quantum field theory. For recent reviews see [Goold, Huber, Riera, del Rio, Skrzypczyk, J. Phys. A: Math. Theor. 49, 143001 (2016)], [Vinjanampathy, Anders, Contemp. Phys. 57, 1 (2016)] and [Millen, Xuereb, New J. Phys. 18, 011002 (2016)].
My current reseach interest within QT lies in fundamental and practical restrictions for thermodynamic processes, specifically, in understanding how various resources -- energy, time, and complexity -- can be used to perform basic tasks relevant for quantum-information processing, e.g., cooling, state preparation, and copying of quantum and classical information, but also how restrictions of complexity (for instance, restricting to Gaussian operations) influence typical thermodynamic tasks such as energy extraction, storage, and distribution, as well as converting work and correlations into each other. More information can be found here. |
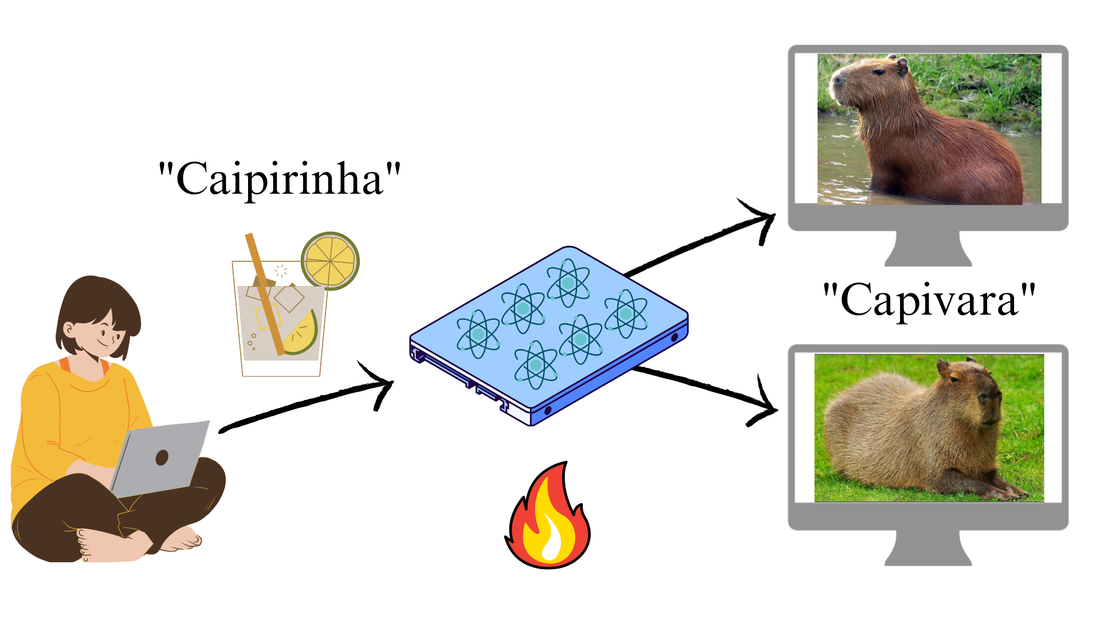
Sonja (named in honour of Brazilian physicist Sonja Ashauer, who was the first Brazilian woman to earn a doctorate in physics) wants to store a quantity of information X (e.g., the word “Caipirinha”), in a memory (M) composed of N subsystems, such that multiple observers can access this information independently. However, if the memory has not been prepared in an ideal (pure) state, here meaning it is prepared in a thermal state, the ability to broadcast information is limited. Different memory subsystems thus
contain imperfect information (e.g., the word “Capivara”).
|
|
Quantum metrology exploits distinctive quantum features, such as entanglement, to enhance the estimation precision of parameters governing the dynamical evolution of the probe systems beyond that achievable by classical means. This enhancement is manifested in the form of a scaling gap in precision with respect to the available resources (the number of probe systems or the average input energy) between the corresponding optimal quantum and classical strategies, and depends on the specific encoding of the parameter in the Hamiltonian describing the evolution.
Here, I have recently been pursuing the question, whether architectures for measurement-based quantum computation can be employed as flexible metrology devices. In this context, we have recently investigated the possibility of creating a versatile all-purpose device for quantum metrology based on 2D cluster states [Friis, Orsucci, Skotiniotis, Sekatski, Dunjko, Briegel, Dür, New J. Phys. 19, 063044 (2017)]. A presentation of this work can be found here (pdf). |
Another research interest in quantum metrology concerns estimation scenarios where the parameter of interest is encoded in Gaussian transformations, see [Friis, Skotiniotis, Fuentes, Dür, Phys. Rev. A 92, 022106 (2015)], and more generally in the connection between quantum metrology, quantum computing and quantum thermodynamics.
For more information see this page.
For more information see this page.