Fermionic Quantum Information

Fermions make up essentially all standard matter in the standard model of particle physics, but interestingly their role in quantum information and computation is sometimes regarded as marginal. Nonetheless, growing interest in fermions and their interesting properties is arising through applications in solid state physics. Many theoretical studies rely on mappings between fermions and qubits - the Pauli principle practically limits the occupation of a fermionic mode to at most one particle, effectively turning them into two-level systems.

Mappings between fermionic Fock spaces (left) and qubit spaces (right) are generally not consistent. Tracing (downward arrows) and mappings between fixed numbers of modes/qubits do not commute.

While isomorphisms between N fermionic modes and N qubits are known, e.g., the famous Jordan-Wigner transformation, the structure of the isomorphisms is not preserved under the partial trace operation. This leads to a mismatch between fermions and qubits. The simple bottom line is "fermions are not qubits".

Read about it in [Friis, Lee, Bruschi Phys. Rev. A 87, 022338 (2013)] or download a presentation [pdf].

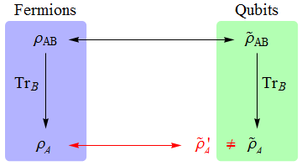
From a field theory point of view, it is natural to consider states of fermions that are superpositions of different particle numbers. However, if unrestricted, such superpositions can lead to weird situations, where the marginals of a bipartite pure state do no longer have the same spectrum, which leads to problems in defining the entanglement in such a system. Fortunately, these problems can be avoided by using arguments from relativity, which enforce a superselection rule that forbids superpositions of even and odd numbers of fermions, see [Friis, Reasonable fermionic quantum information theories require relativity, New J. Phys. 18, 033014 (2016)].

In our new paper "Teleporting quantum information encoded in fermionic modes", just out in Physical Review A 101, 052326 (2020), we take a closer look at the influence of superselection rules on teleportation (and what it even means to "teleport") using fermionic mode entanglement.